Improved formulas for magnetics core loss with duty cycle effects.
Introduction
As modern power converters move towards higher efficiency, it is essential to have better models for all of the loss mechanisms in your components. In the first part of this article, we talked about the need for a single continuous equation to match the empirically-measured losses. In this second part, the effect of different waveforms and duty cycle are incorporated into the modeling.
Magnetics B-H Loops
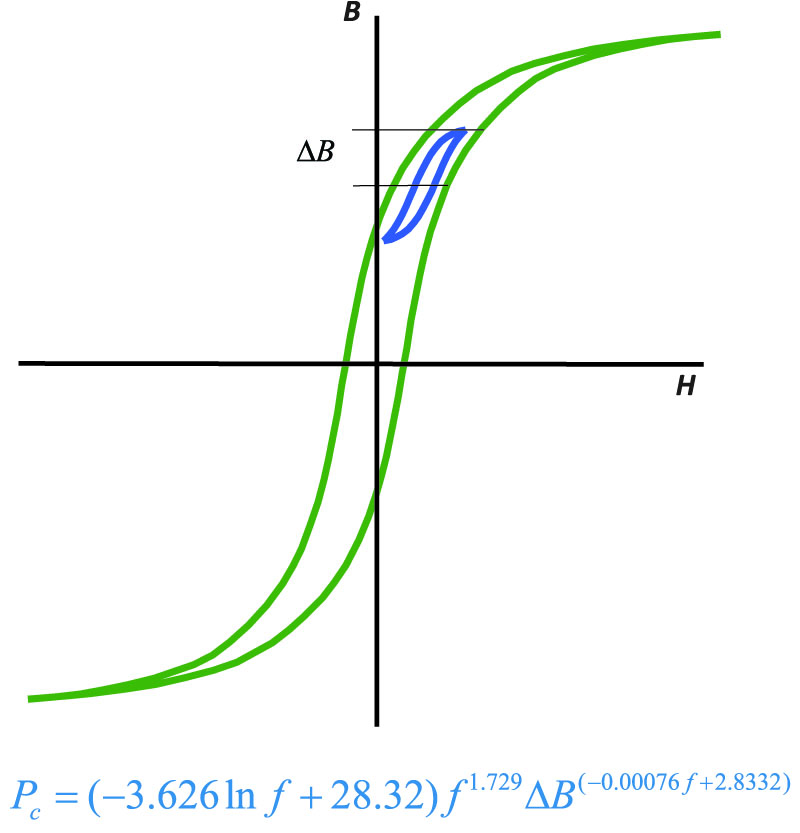
Part I of this article [7] showed how a single adaptive equation could be used for predicting the core losses of a ferrite material. Figure 1 shows the hysteresis loss mechanism for a core, and gives the specific equation for the Magnetics “R” material. The equation adapts itself to the changing slope of the curves with frequency, and avoids the need for discrete changes to the equation with different frequency bands.
Figure 1: B-H Loop for a High-Frequency Material with Core Loss Equation for R Material
Sinusoidal Core Excitation
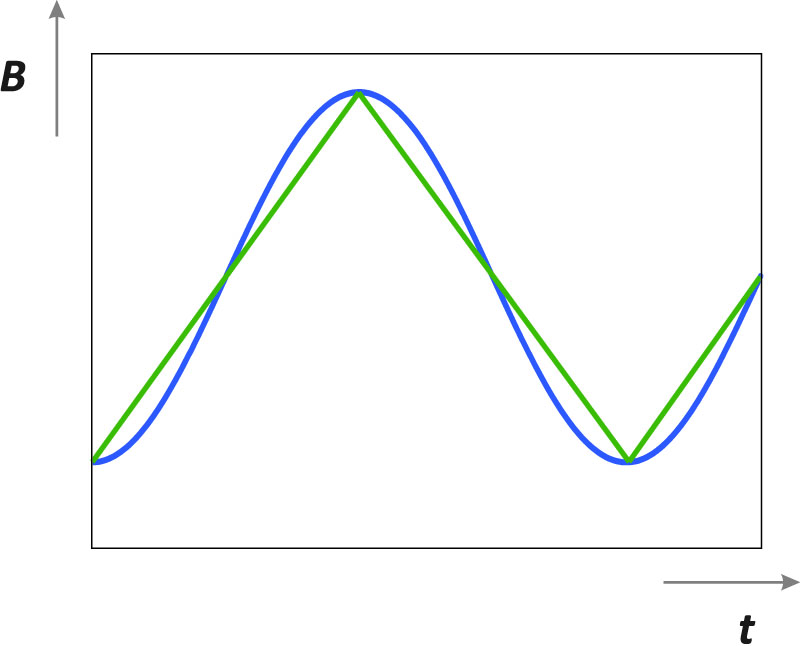
All core loss curves are measured using sinusoidal excitation. However, in squarewave converters, the excitation of the core is not sinusoidal at all. As is shown in Figure 2, a 50% square wave voltage drive results in a triangular current waveform in the inductor, and a triangular waveform for the core excitation.
This does not mean that the measured loss curves are not useful. Mr. Rudy Severns demonstrated many years ago that the difference in loss is very small between a sinusoidal excitation and a 50% triangle wave. The small difference is certainly less than the experimental error in making the loss measurements.
The waveforms of Figure 2 give an indication of why this happens. For part of the waveform, the sinusoidal curve has a lesser slope than the triangular, and for other parts, the slope is greater. The core loss is a function of dB/dt, and as we will see further on, the changes in loss will not be large.
Figure 2: Sinusoidal and 50% Duty Cycle Triangular Waveforms
Converter Waveforms with Duty Cycle
Although there is little difference in loss with a 50% triangle wave and a sinusoid, in many converters we find waveforms of quite different duty cycles. This can increase the core loss considerably. As more and more designers work with wide input ranges, they may find their transformers and inductors getting considerably warmer than expected.
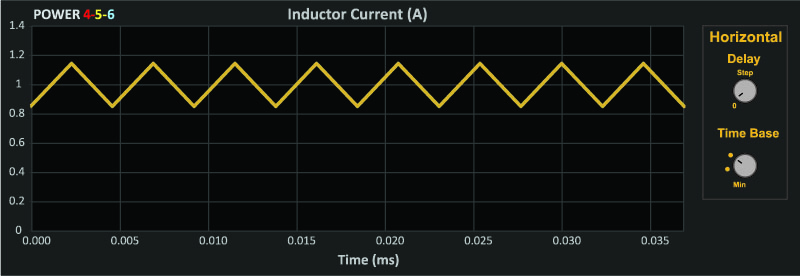
Figure 3: Buck Inductor Current with 50% Duty Cycle
Figure 3 shows a buck converter inductor operating with a 50% duty cycle, corresponding to low-line operation. (Please note: All waveforms shown in Figures 3-5 were generated by the design program POWER 4-5-6 [1].)
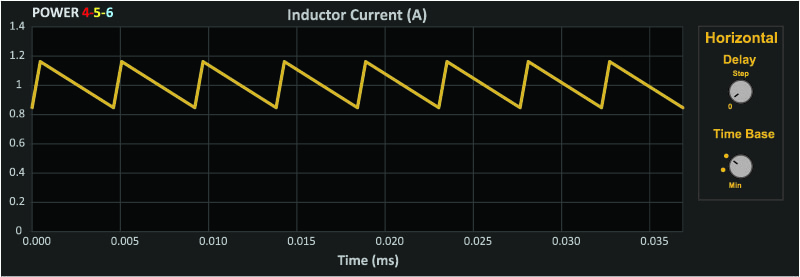
At high line, Figure 4 shows the inductor current running with just a 10% duty. In this case, the change in B with respect to time is 5 times higher than the 50% duty cycle case, and higher core losses can be expected.
Figure 4: Buck Inductor Current with 10% Duty Cycle
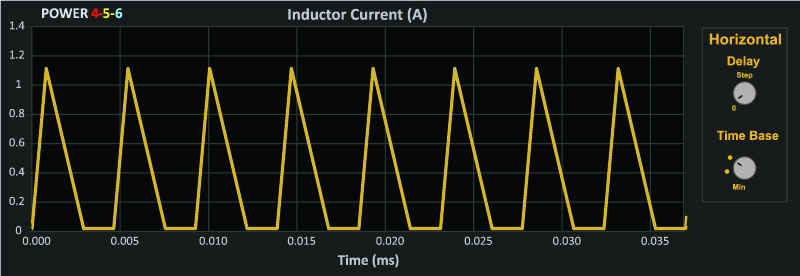
Figure 5 shows a more extreme case where the inductor current is discontinuous. In this case, the rise time and the fall time of the flux in the core will both be much higher than the 50% case, and core loss will be even higher.
Figure 5: Discontinuous-Mode Inductor Current Waveforms
“Apparent Frequency” Loss Calculations
It was discussed by Cliff Jamerson [2] that the increased loss with fast rise and fall times can be addressed with the method of apparent frequencies. If we look at the rise time of the flux relative to the 50% triangle wave, we can assign a frequency which should be used to look up the core loss value. Similarly, we can do the same thing for the fall time.
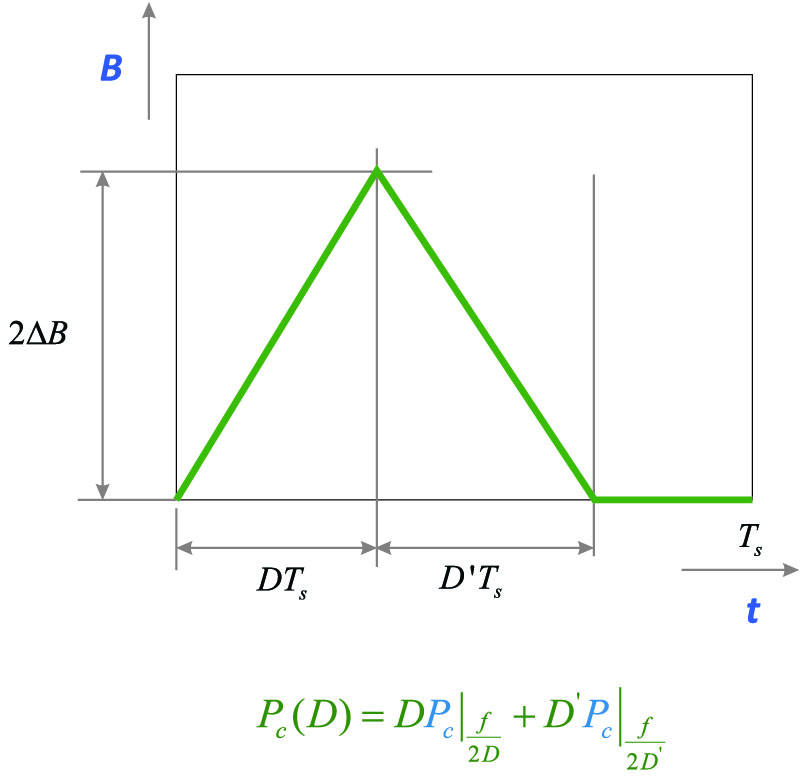
Figure 6 shows the generalized waveform for either continuous conduction mode or discontinuous conduction mode, and gives the modified loss equation according to the calculated apparent frequency for each case. This equation has been incorporated into the design program POWER 4-5-6 to give much more accurate predictions of core loss.
Figure 6: General B vs T Waveform with Modified Core Loss Equation
Core Loss Multiplier Results for R Material
Since all core materials have their own loss characteristics, it is not possible to plot a general curve showing the loss multiplier for different duty cycles. We can only generate specific cases for each material. Even then, the multiplier only applies for the given operating point for ΔB since the core losses are strong nonlinear functions.
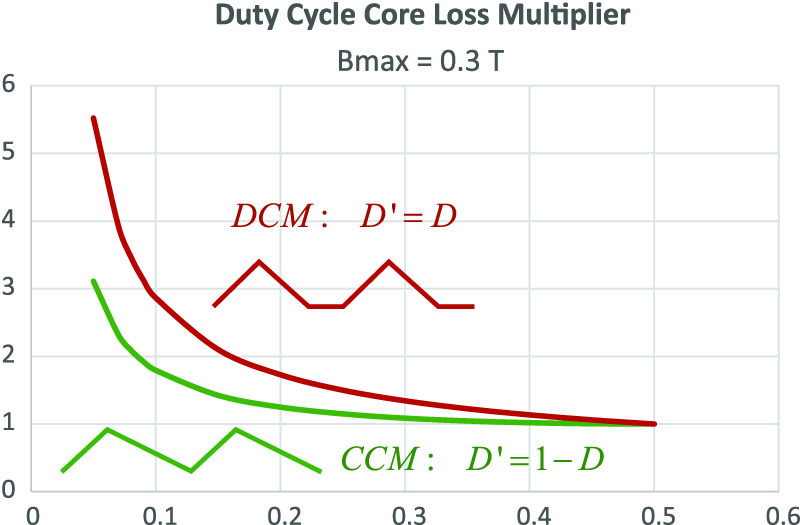
Figure 7 shows the results of the loss multiplier for R material with different duty cycles, for either CCM or DCM. It can be seen that for moderate deviations away from 50% duty, the increment in loss is small. Only when we get down to very low duty cycles does it become very significant. For example, at a 10% duty cycle in DCM, the core losses are multiplied by almost three. In CCM, a 10% duty cycle produces about a 70% increase in core loss.
Figure 7: Core Loss Multiplier with Different Duty Cycles in CCM and DCM
Summary
A core loss equation has been derived for converter waveforms where the duty cycle of the flux waveform is less than 50%. This is used in conjunction with an improved adaptive form of the Steinmetz equation for the R material ferrite from Magnetics. At low duty cycles, the loss can be multiplied a more than a factor of 3, making such calculations essential for wide range converters.
References
Simulation and Design Software POWER 4-5-6 incorporating Ridley-Nace core-loss equation http://www.ridleyengineering.com/software/POWER_4-5-6_Manual.pdf
Targeting Switcher Magnetics Core Loss Calculations, Clifford Jamerson, Consultant, Power Electronics Technology, Jan 2001.
Power supply design articles http://www.ridleyengineering.com/design-center.html
Join our LinkedIn group titled “Power Supply Design Center”. Noncommercial site with over 7000 helpful members with lots of theoretical and practical experience.
See our videos on power supply design at http://www.youtube.com/channel/UC4fShOOg9sg_SIaLAeVq19Q
Power supply design workshops including magnetics design http://www.ridleyengineering.com/workshops.html
Adaptive Modeling Equation for Core Losses, http://www.ridleyengineering.com/design-center.html Article [89] Core Loss Modelling