What happens when the input filter is poorly designed.
Introduction
In this article, Dr. Ridley continues the discussion of power supplies with input filters. He shows how the presence of a poorly-designed filter has a drastic effect on the loop gain of a voltage-mode controlled system. He also shows that the loop gain of a current-mode system can be a poor indicator of stability when an input filter is connected to the system.
Impedance Interactions
As discussed in the previous articles of this series [1], an input impedance measurement gives information about the characteristics of the power supply's input terminals. We use this information in conjunction with measurements of the output impedance of the input filter to assess whether a system interaction is likely to occur. This is important since it can lead to instability of the power supply.
Fig. 1: Power supply with input filter module. A damping network is used to control the output impedance peaking.
Figure 1 shows a power supply with an input filter. As shown in the last article of this series [1] a damping network is often needed to control the peaking of the output impedance of the filter.
Middlebrook's important work on input filter interactions showed that if the output impedance of the input filter is always less than the input impedance of the power stage, there would not be any instability caused by the presence of the input filter. This is a very important result since it allows us to analyze the power stage completely separately from the input filter. Switching power supplies are difficult enough to analyze and control, and Middlebrook recognized that engineers really don't want to extend their analysis further to include multiple reactive components of the input filter. He wanted to keep the math simple.
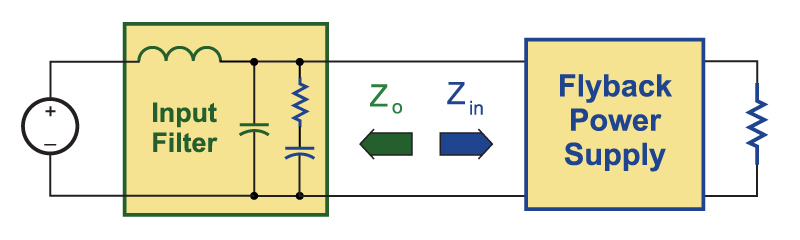
Figure 2 shows measurements of a power supply input impedance, compared with the output impedance of two different filter designs.
Fig. 2: Comparison of measurements of power supply input impedance and input filter output impedance. With an undamped filter, the output impedance exceeds the input impedance of the power supply.
The first output impedance, shown in red, is for an undamped filter. It can be seen that the output impedance is higher than the input impedance of the power supply. The second curve shows the output impedance for the same filter elements with a 10 ohm resistor in series with a capacitor connected across the output of the filter. For the damped filter, there is a good separation of the output impedance of the filter and the input impedance of the power supply, which is the desired design result.
Voltage-Mode Feedback Loop Gain Measurements
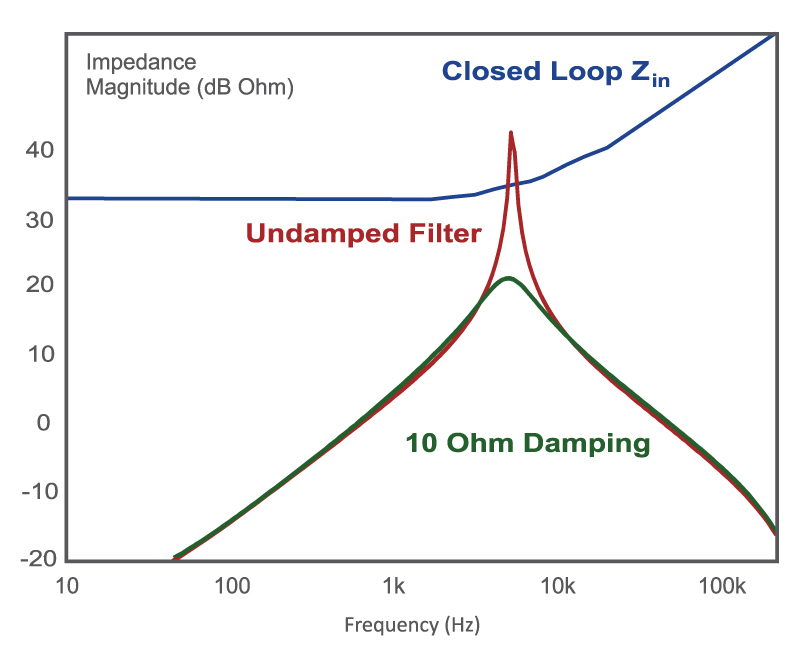
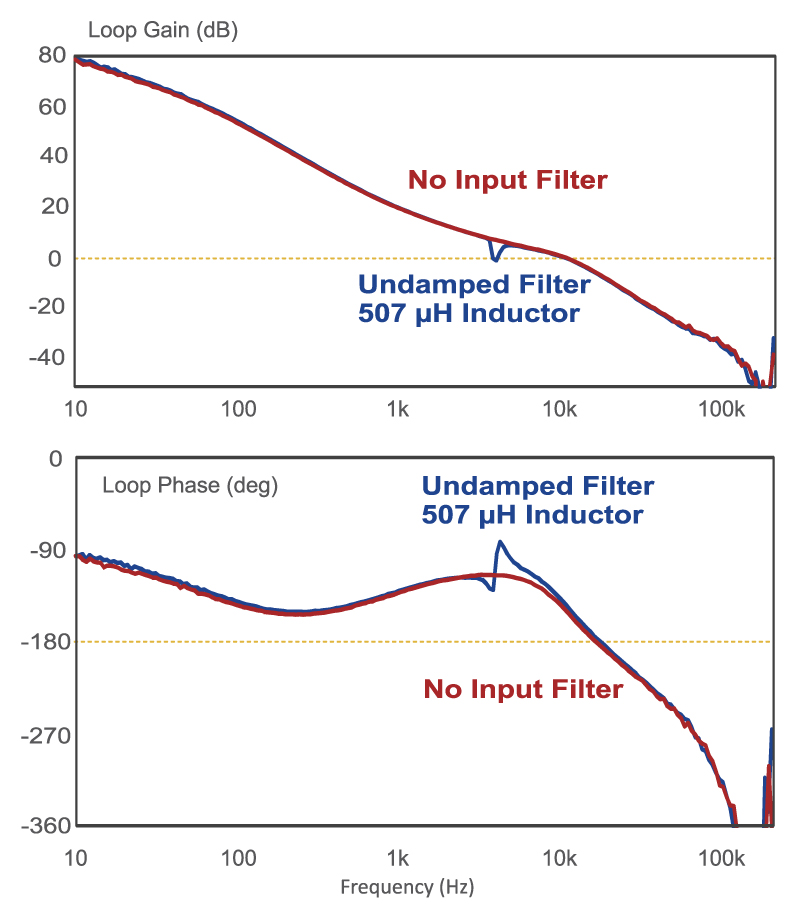
It is instructive to look at the loop gains of the power supply to see how the presence of the input filter affects that measurement. Figure 3 shows the voltage-mode control loop for the system of Figure 1, both with and without a filter.
Fig. 3: Voltage-mode control loop gain with an undamped input filter.
The red curve of Figure 3 shows loop gain without a filter added. The crossover is at around 6 kHz, and there is a phase margin of about 50 degrees.
Adding the undamped filter has a dramatic effect on the voltage-mode loop gain. There is a notch in the gain, and then the high frequency part of the loop gain follows the same curve as the system without a filter. However, the phase at the notch frequency drops dramatically – ending up with an additional phase delay of 360 degrees! This large drop in phase is due to an additional pair of poles caused by the input filter, and a pair of complex RHP zeros.
Trying to analyze this complete system with four poles, three zeros, and three additional control states is not something that you really want to do. Hence the Middlebrook criteria – you can avoid this unpleasant math by just looking at the impedances and making sure they are well separated.
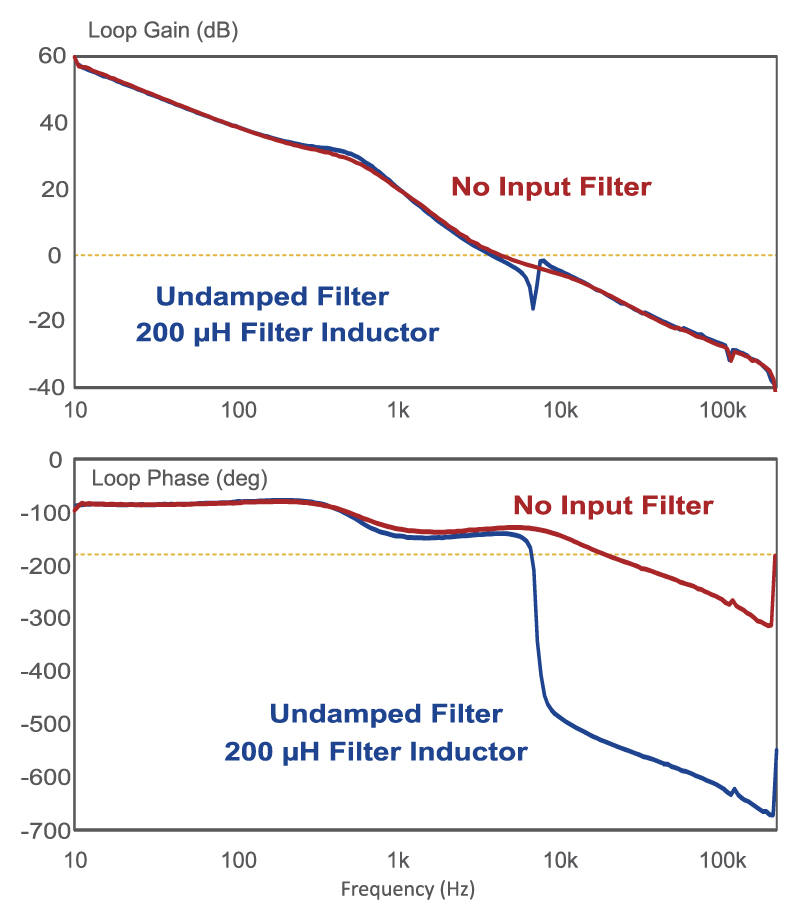
Fig. 4:Voltage-mode control loop gain with a properly-damped input filter.
Figure 4 shows the loop gain of the voltage-mode system with a properly damped input filter. In this case, there is no overlap of impedances, and the effect on the loop gain is much less dramatic. Although there is still a small notch in the gain, the phase does not exhibit the same dramatic drop as for the system with the undamped filter.
Clearly, from looking at Figures 3 and 4, we can assess the impact of the input filter on the overall power system.
Current-Mode Feedback Loop Gain Measurements
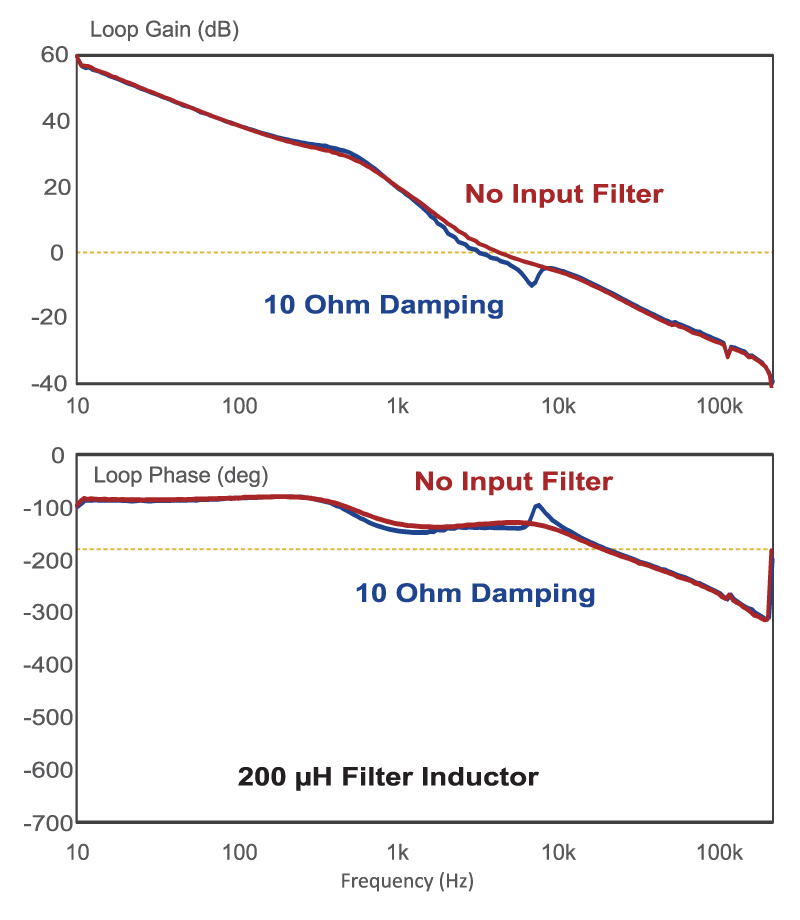
The situation is not so straightforward when we look at the loop gain of a current-mode controlled system. The red curve of Figure 5 shows a well-designed feedback loop with a crossover frequency of close to 10 kHz, and plenty of phase margin. When the undamped input filter is added, there is not much of a change to the loop gain.
Fig. 5: Current-mode control loop gains without a filter and with an undamped input filter. The current-mode loop gain is not a good indicator of the stability of the system with the input filter.
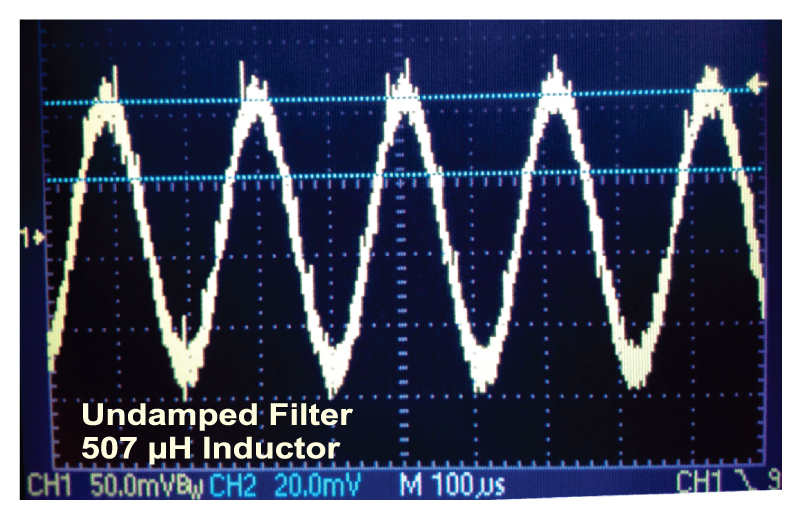
The loop gain of Figure 5 predicts that the system is stable when in fact there is oscillation in the system. Figure 6 shows the voltage waveform at the output of the input filter (ie the input of the power stage). There is sustained ringing at this node of the circuit, but it cannot be observed at the output of the power supply at all.
In control terms, this is what we call an unobservable system. You cannot see disturbances on the input rail when you look at the output voltage. Oscillations at the input bus are immediately adjusted for by the current-mode modulator, and the output remains regulated.
Fig. 6: Despite the apparently-stable loop gain, oscillations can be seen in the current-mode system.
This is not a good way to design your power system. It is crucial that input impedance and filter output impedance measurements are measured to ensure that there will not be any instability. Looking at the loop gain is not sufficient to guarantee that the system will be stable.
This is something of an alarming situation. Most switching power supplies are designed with current-mode control. Most switching power supplies are also designed with input filters. Most designers do NOT make measurements of input impedance and filter output impedance, leaving themselves at risk of instability even if they are making loop gain measurements.
The reason this does not happen too frequently is that filters have been designed in the past with large electrolytic capacitors. The characteristic output impedance of the input filters with large capacitors is inherently low, greatly reducing the risk of input impedance interactions. For modern capacitor technologies, a small-value MLC capacitor can carry all of the necessary switching current, and the input filter impedance can be much higher.
Summary
This article discusses how input filter impedance interactions have a dramatic effect on the loop gain of a voltage-mode controlled system, introducing an additional 360 degrees phase delay in the loop if the filter is poorly designed. Proper damping of the input filter is needed to make sure the system is stable.
For current-mode control, it has been shown that filter interactions are far more difficult to detect with the loop gain measurement, and a system can have an apparently good loop gain while exhibiting oscillations. It is very important to make sure loop gains and impedances are measured to ensure a stable power system.
References
- Join our LinkedIn group titled “Power Supply Design Center”. Noncommercial site with over 7000 helpful members with lots of theoretical and practical experience.
- For power supply hands-on training, please sign up for our workshops.
- Ridley Engineering Design Center, www.ridleyengineering.com/design-center.html, Articles [59-61] "Input Impedance Measurements and Filter Interactions."