Papers from MIT and others indicate a current loop gain of infinity under all conditions, clearly an impossibility according to Nyquist.
Introduction
In this article, Dr. Ridley shows how a third way of defining average current leads to an infinite gain of the modulator gain for current-mode systems. Another simple derivation produces a fourth expression for the modulator gain, thus completing the set of gains to be found in the literature.
Different Current-Mode Modulator Models
In the first part of this series on current-mode control, it was mentioned that several researchers considered the inductor to be a current source since its peak value was directly set by the control voltage into the modulator. This is an implicit assumption of infinite gain in the current loop, otherwise the current source would not be ideal.
Other researchers, including Drs. Middlebrook and Lee, did not regard the gain around the current loop as infinite, recognizing quite correctly that the controller set the peak value of the current exactly, but not the average level. In the last two parts of this series, we showed how the average value could be defined in two different ways, and these definitions of average current give rise to the modulator gains that were found by Middlebrook and Lee in their work.
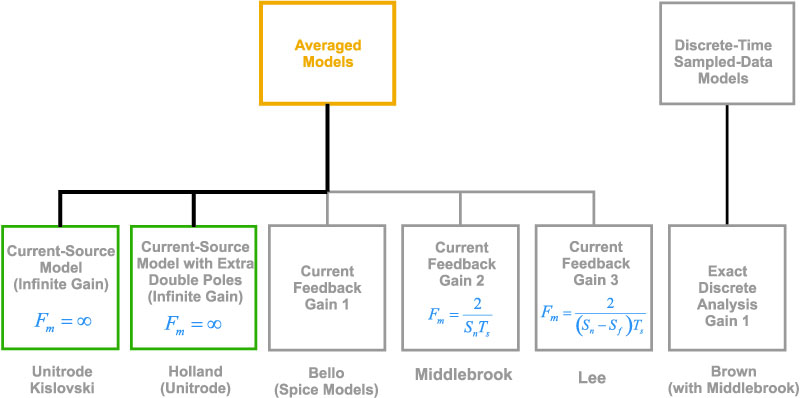
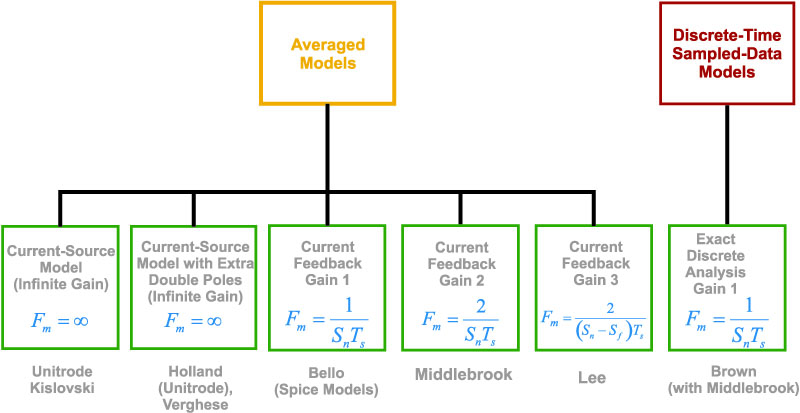
Figure 1 below shows a table of the different analysis approaches and the equivalent gains of the modulator. So far we have three different expressions for the modulator gain. In this part of the series, we will show how a third definition of average current leads to the infinite value of modulator gain, thus vindicating the current-source models.
Figure 1: Different Models for the Modulator Gain
Infinite Modulator Gain Derivation
Middlebrook, in defining his average current, set it to be one-half of the inductor current upslope, and this seems like a reasonable way to do it. The current during the downslope was ignored. Lee took both the upslope and the downslope into account, and defined the average current as the mean of two discrete values: the initial perturbation in the current and the final perturbation of the current. In Lee’s original papers, it was not explicitly done this way, but rather with describing function techniques. However, the resulting modulator gain is the same. Note: there is nothing inherently wrong with either of these techniques, they are arbitrary definitions of what average current should be.
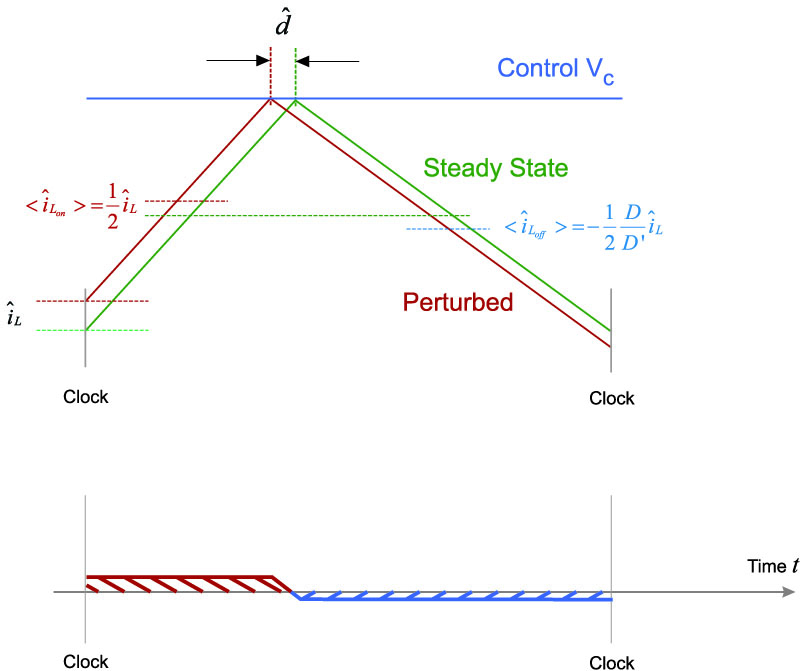
A third definition of average current is also possible. Instead of just averaging the discrete values of current perturbation at the beginning and end of the switch cycle, we can look at all the values of the current over the cycle. This is illustrated in Figure 2. The blue shaded area of the figure, and the red shaded areas are added together, with the red area being negative.
Figure 2: A Third Definition of Average Current
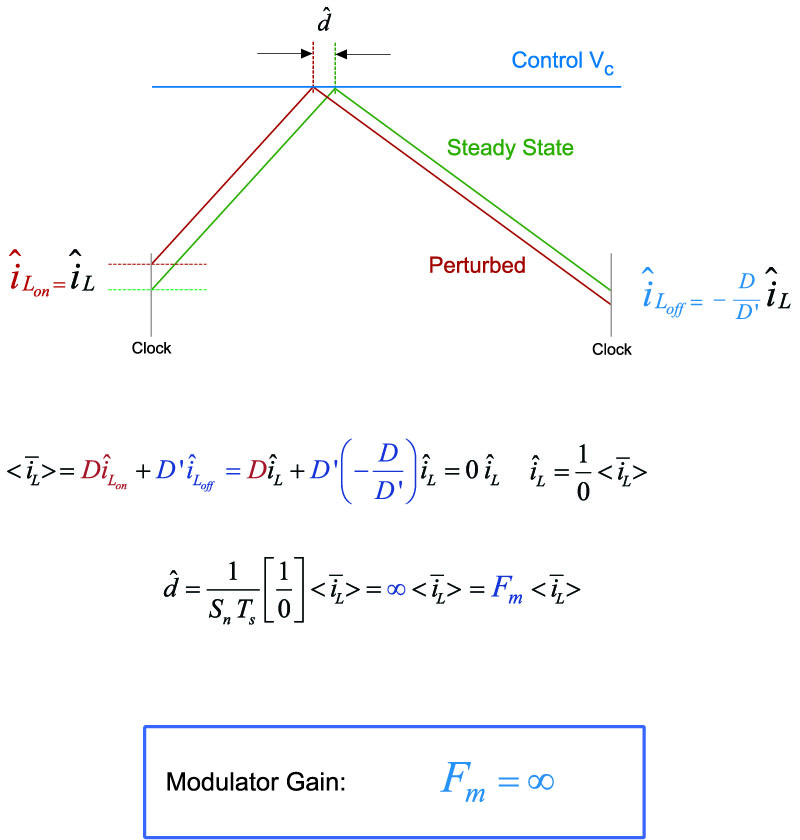
The calculations for this situation are derived in Figure 3. A curious result occurs here – regardless of the duty cycle, the average perturbation of the current as defined this way is always zero! That means there is no perturbation in the average current with this definition, and the inductor is therefore behaving as a true current source. Another way of looking at this is to say that there is a small change in duty cycle, but zero change in current, so the gain of the modulator from current to duty cycle is therefore infinite.
Figure 3: This Definition of Average Current Leads to Infinite Modulator Gain
The infinite modulator gain has been approached in the literature several times. It was proposed early on in the history of current-mode by Kislovski, Holland, and others, and again in the early 1990s by Verghese at MIT. We will see later how well the infinite-gain model holds up when we look at real working hardware.
Final Simple Modulator Gain
There is one more variation of modulator gain that is to be found in the literature. This version is very simple and straightforward to derive, and it was originally used in early Spice models by Vincent Bello. It was also used by Dr. Art Brown of Caltech when he wrote his seminal paper and dissertation on current-mode control.
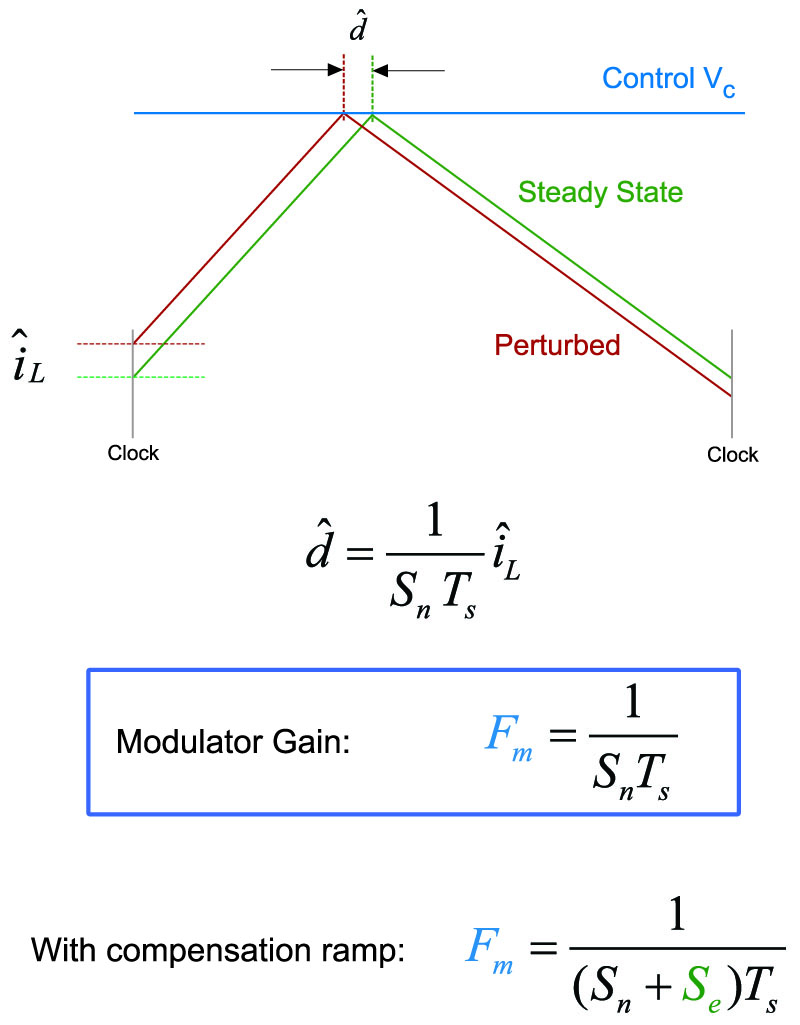
Figure 4 shows the modulator waveforms and definitions for this final version of gain. Instead of trying to define an average current with one of the many ways to do this, only the initial perturbation in current is considered in deriving the small-signal gain of the modulator.
The gain is now defined in exactly the same way as voltage-mode control. It is simply given by the reciprocal of the equivalent ramp height of the signal coming into the modulator. Since this is not a sawtooth waveform, the ramp height is given by the sum of the current slope and compensating ramp slope, multiplied by the switching period.
Figure 4: Simple Modulator Gain Considers Just the Initial Current Variation
Complete Set of Models in Literature
We have now derived all of the modulator gains that are to be found in the literature on current-mode control. (A modern and very complex treatment of the problem by Dennis Feucht tried to give an expression to combine all versions into one complex model, but there is no way to reconcile such different results.) All of the papers you might find on current-mode control will be using one of the four modulator gains in their model.
Figure 5: Complete Set of Modulator Gains Found in Literature
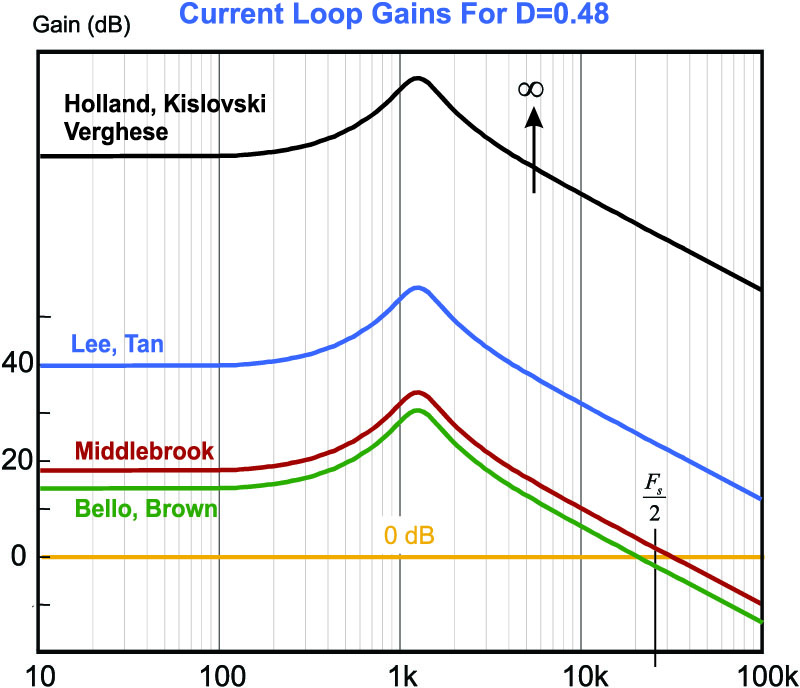
We can show the effect of each of these modulator gains on the current loop gain of the system. This is shown in Figure 6. Notice that there is a wide disparity in the results. The simplest model, corresponding to the reciprocal of the ramp height, predicts a crossover frequency at about 1/3 of the switching frequency. This is the only model to show that the current loop will cross over below half the switching frequency. Middlebrook’s model crosses over at 2/3 the switching frequency. Lee’s model, and the infinite gain model, cross over at much higher values.
Figure 6: Plot of Current Feedback Loop Gains with All Modulator Values
This set of results is key in understanding why there remains such widespread confusion in the power supply industry about how to model current-mode control. Many very well-respected researchers found very different results for the same quantity, and there has never been an explanation of what might have gone wrong. Only one of the predictions for modulator gain can be correct. In the final part of this series we will not only show which is correct, but also where all of the incorrect versions made a common assumption that leads to the wrong result. Once this assumption is corrected, the entire topic of how to define the average current properly becomes immaterial, and all definitions will converge to the same result for modulator gain.
Summary
In this article, we have shown two more derivations of modulator gain. This results in four completely different results, and this has really confused the industry about how modeling should be done for current-mode systems. Next in this series, we will show how a simple erroneous assumption leads to all the different versions of modulator gains, and how it can be easily corrected so that the different definitions of average current are no longer important. This final step will be the first time that the result has been published.
References
[1] "A Unified Analysis and Design Procedure for a Standardized Control Module for DC-DC Switching Regulators”, F.C. Lee, Y. Yu, M.F. Mahmoud, "A Unified Analysis and Design Procedure for a Standardized Control Module for DC-DC Switching Regulators," Power Electronics Specialists Conference, 1980 Record, pp.284-301.
[2] “Topics in Multiple-Loop Regulators and Current-Mode Programming”, R.D. Middlebrook, IEEE Transactions on Power Electronics PE-2(2) pp.109 – 124, April 1987.
[3] “A New Small-Signal Model for Current-Mode Control”. Full original version available as a free download at www.ridleyengineering.com/books.html. Updated color version available from Researchgate.
www.researchgate.net/publication/280491161_Current-Mode_Chapter_1 www.researchgate.net/publication/280491229_Current_Mode_Chapter_2
www.researchgate.net/publication/280682067_Current-Mode_Chapter_3
[4] "Topics in the Analysis, Measurement, and Design of HighPerformance Switching Regulators", A.R. Brown, PhD. Dissertation, California Institute of Technology, May 15, 1981.
[5] "Modeling, Analysis and Compensation of the Current-Mode Converter",B. Holland, Powercon 11, 1984 Record, Paper H-2.
[6] Power supply design articles www.ridleyengineering.com/design-center.html
[7] Join our LinkedIn group titled “Power Supply Design Center”. Noncommercial site with over 6500 helpful members with lots of theoretical and practical experience.
[8] See our videos on power supply design at www.youtube.com/channel/UC4fShOOg9sg_SIaLAeVq19Q
[9] Learn about current-mode control in our Power Supply Design Workshops www.ridleyengineering.com/workshops.html