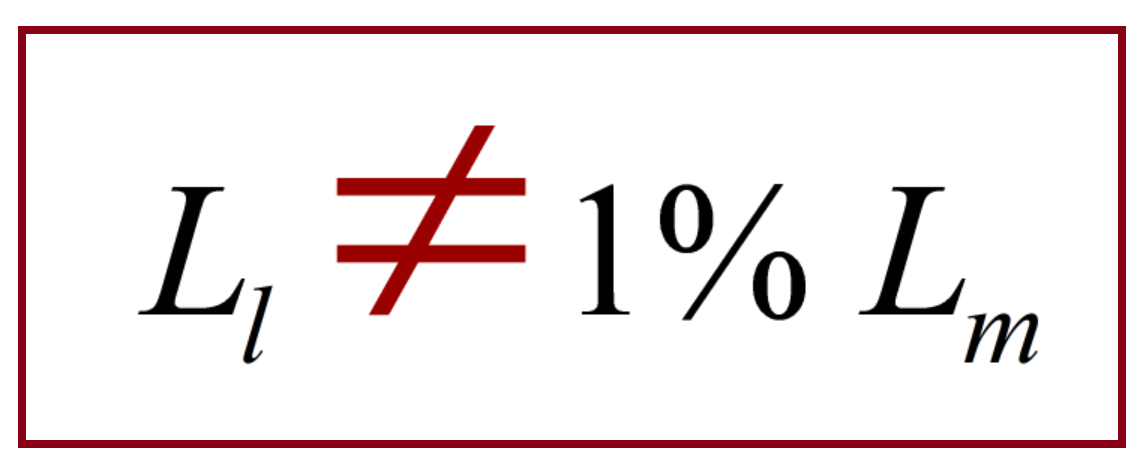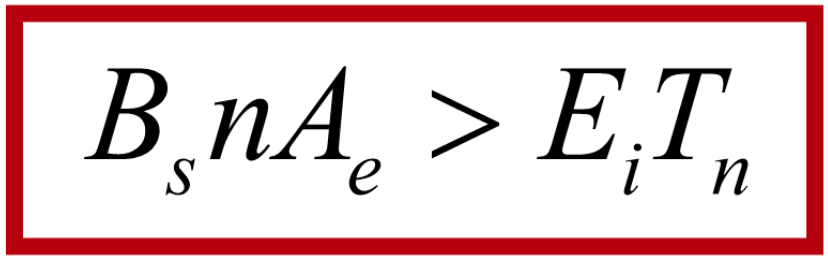One equation governs the saturation of a transformer, but the leakage inductance provides strong direction to a design.
Magnetics Design – Lessons Learned
After graduating from college, my first job was for a computer company outsideBoston. The project was to make a production power supply for computers using a full-bridge design at 850 W. These were the early days of FETs, so we were taking switching frequencies from the industry-standard 20 kHz or so to 100 kHz. The basic specifications were as follows:
Input voltage: 85 VAC to 265 VAC (300 V surge for 1 second)
Output Voltage: 5 V at 130 A (with margin to 5.25 V)
+ 12 V at 7 A
- 12V at 7 A
There was no PFC circuit in front of the full-bridge.Nobody had thought of that at the time, and there were certainly no control chips for PFC. This meant that the stresses on the full-bridge topology were quite high, with operation over an almost 3:1 range.
Very few FET full bridges had been built for production at the time, we were all just learning from experience. The design of the transformer was assigned to my mentor at the time, Dan Balulescu, since he was from the power utility industry and had some experience. (A warning for everyone – once you have experience in magnetics design through to production, you will always be the one that they call on!)
Dan spent many days in his office, buried deep in magnetics design notes, data sheets, and page after page of calculations. Finally, he emerged from the office, showed me the design, and it was sent off to be fabricated by the local magnetics manufacturer. The secondary of the transformer consisted of two turns of 20 mil foil, center-tapped with another two turns, so construction of this was not something we could do ourselves. We needed a professional company to handle the foil construction, the litz primary, and the full safety insulation for VDE approval.
Dan, of course, knew all about the one equation for design that we talked about in the last article of this series. He had the appropriate number of turns for the core selected. And, like many designers, he had a myriad of other equations to try to achieve an optimal design. It was a very painstaking process.
We were fully engaged in board layout, controller design, thermal design, packaging, and everything else that goes into a real-world power supply for several months. The first transformer showed up about a month after the initial design was started.It was my job to install the transformer on the board, and to begin the circuit board testing. When the switches were all turned off at any significant load, there was a strong ringing on the drain of the power FETs. At low line, there was so much energy in this ringing, the voltage rang up to the opposite rail, clamped through the diode of the opposite FET, then rang down again all the way to the bottom rail. This was a destructive situation. Force commutation of the antiparallel diode of the FET led to failures of the bridge.
There was a lot of pain in the lab. The IR rep was called in several times to bring more samples of the FETS (no Digikey existed!) Finally I told Dan – “The transformer has too much leakage – I cannot make it work in our circuit.”
He seemed somewhat unsurprised as though he had anticipated this might happen. This was my first big lesson in the real world – despite all the textbooks in the world, all the guidance, your power circuit is unique. You cannot fully anticipate every parasitic and every event that you are going to see. There will be design iteration, so expect this and be ready for it.
The next transformer cut the number of turns in half and increased the area of the core. This confused me – all that calculation, and after a test we are going to make such a drastic 2:1 change? But there was no choice – the only step down from two turns was one. All the optimization went out of the window. Trial and improvement are the name of the game. We will come back to this point later as it has a big impact on design direction.
Basic Power Transformer Construction
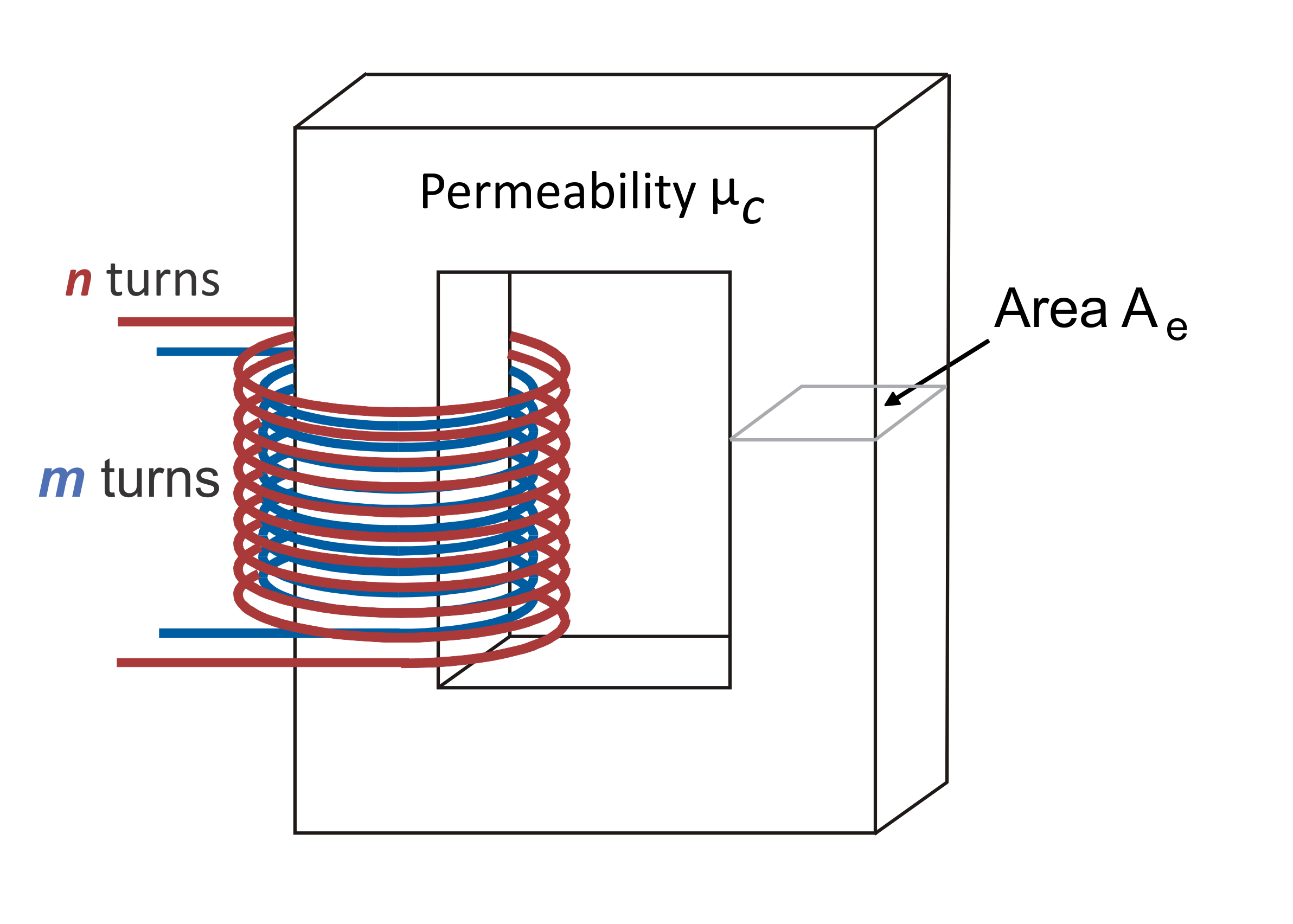
Figure 1 shows the basic construction of a transformer. For high-frequency, hard-switched converters, it is important to get good coupling of primary and secondary windings, so one winding is right on top of the other. (By contrast, a 60 Hz transformer on this shape of core commonly puts one winding on one side of the core, and one on the other. In this case, the high leakage created can actually be beneficial for protection of the system.)
Figure 1: High-Frequency Transformer Construction
The core shape shown here is a U-Core, but that is not important. We need to ensure that we have a closed magnetic circuit, and the actual shape and cross-sectional profile can vary widely. However, the concepts in this article remain the same. We are going to see that the leakage inductance that caused me so much pain in my first design is a function of the spacing between the primary and secondary windings. Small dimensions can make a big difference. Skill and repeatability are crucial in transformer manufacturing.
Power Transformer Equivalent Circuit
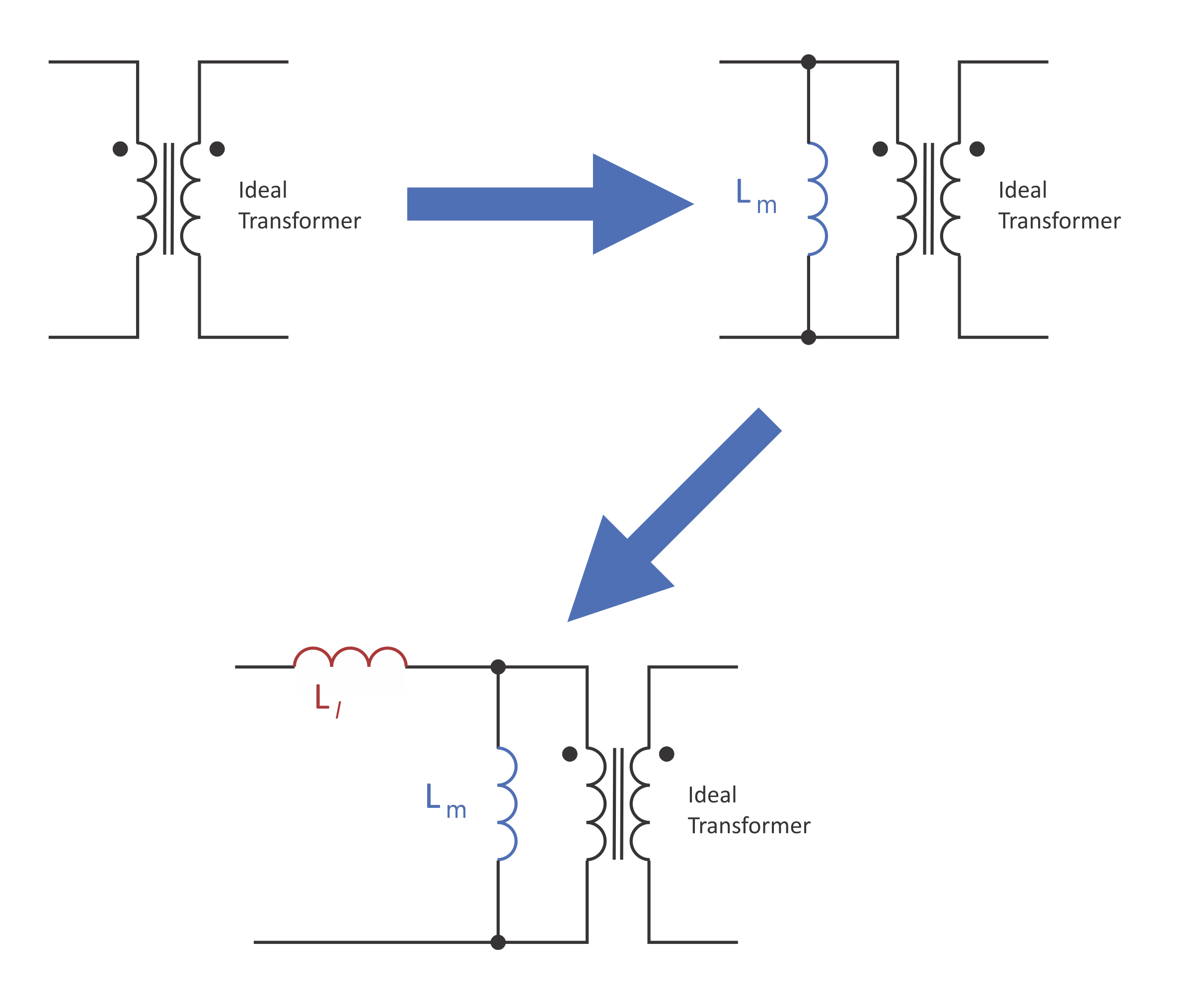
As we learned in the last article, it is not possible to make an ideal transformer. The most important extra element that forms the model of the transformer shown in Figure 2 is the magnetizing inductance, Lm, shown in blue. Preventing this inductance from carrying too much current and subsequently saturating the magnetic material led to the one design equation for a transformer. If the equation is satisfied, the transformer will not saturate.
However, while this one equation must ALWAYS be satisfied, an additional consideration on the leakage of the transformer will guide the choice of core and hence number of turns. The additional circuit element that must be added to the transformer model is leakage inductance, Ll,shown in red in Figure 2.
Figure 2: Transformer Equivalent Circuit with Leakage Inductance. We now have two inductors and an ideal transformer representing the real transformer.
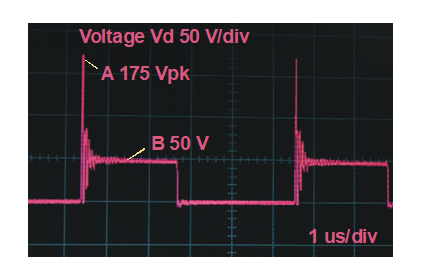
The effect of the leakage inductance on the circuit operation is easy to see, and it can be severe. As you can see from Figure 3, the output diode on this particular secondary is supposed to see just 50 V. However, there is a spike of 175 V due to the leakage inductance ringing with the diode capacitance. Anyone who has built a transformer-isolated circuit is painfully aware of the magnitude of this effect.There is always a desire to lower the leakage in the transformer. Before we can do this, however, we need to know the quantities in the transformer that affect the leakage.
Figure 3: The Effect of Leakage Inductance on Circuit Waveforms with Hard-Switched Circuits
Calculating Leakage Inductance
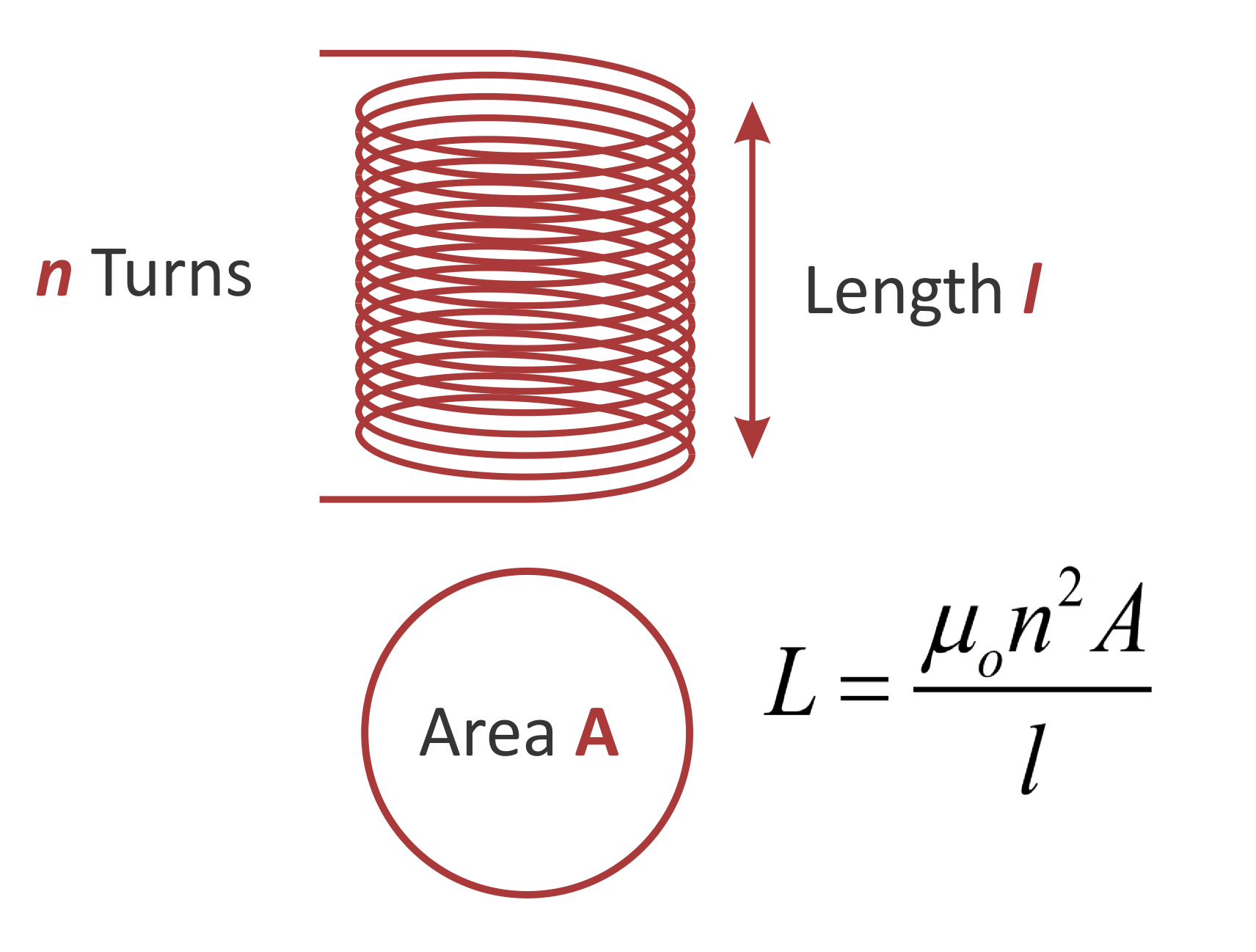
Leakage energy is related to the fields that exist between the two windings of a transformer. No core material is involved, since the fields exist in the space. Hence the equation for leakage inductance is similar to the simple equation for an air-core solenoid, which is well known from basic physics.
Figure 4: The Simple Equation for the Inductance of an Air-Core Coil
Figure 4 shows the basic construction of a “long” solenoid. From basic electromagnetic equations, the inductance of this structure is given by the equation of Figure 4. We can see that the inductance is proportional to the square of the number of turns, the area enclosed by the coil, and inversely proportional to the length of the solenoid.
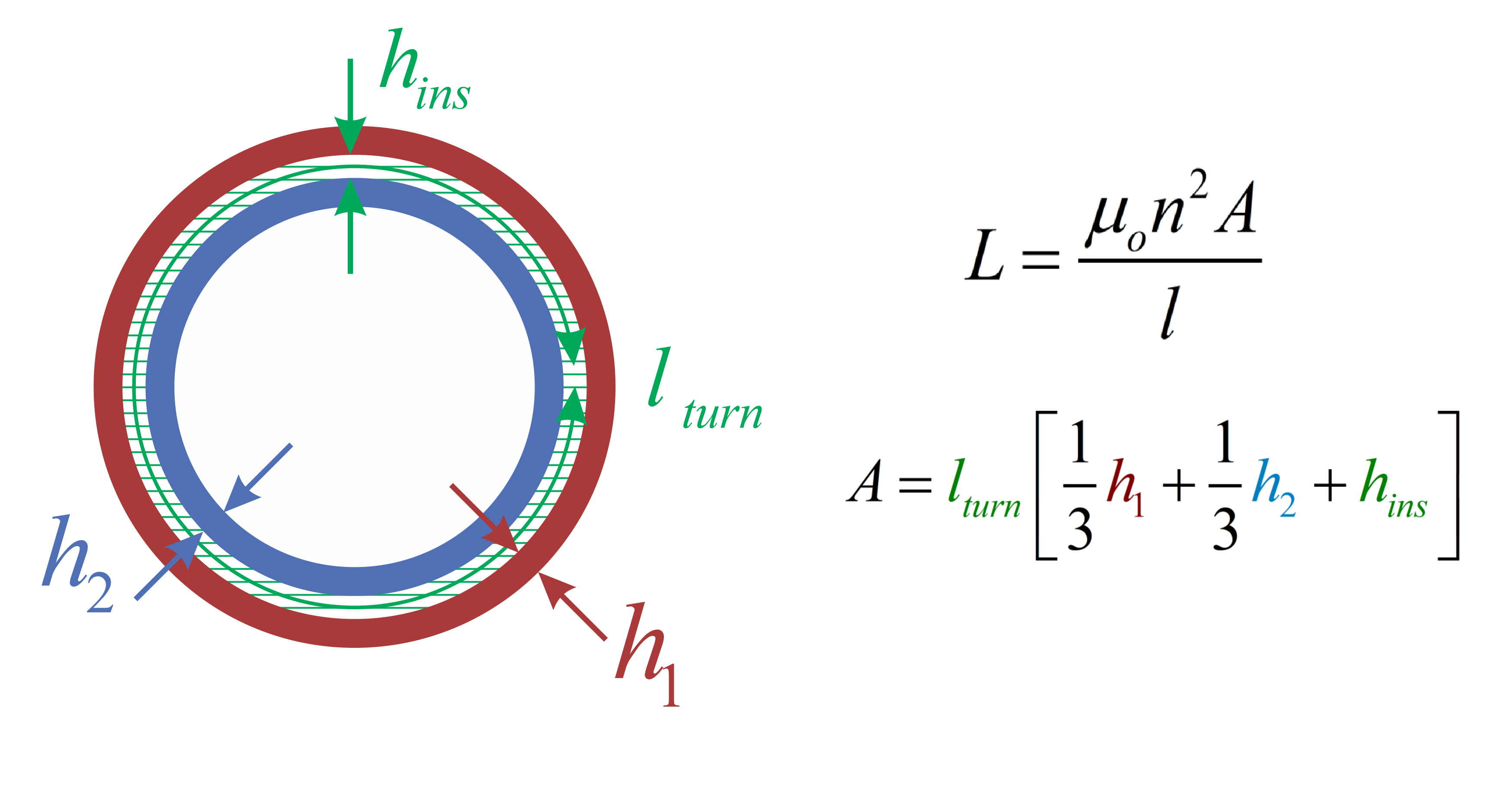
However, we don’t quite have this exact situation in a transformer. We have one solenoid (or winding) inside another. The situation created by this structure is shown in Figure 5 as viewed from above. The red and blue circles are the primary and secondary windings. The green shading represents insulating material, which could be magnetics tape, air, or some other insulator. As you can see, the fundamental equation is the same as for the air core except for the definition of the area.
Figure 5: The Equation for the Leakage Inductance of a Transformer is the Same as an Air Core
The area is no longer the full circle contained by a winding, it is now modified to be the equivalent area betweenthe windings. As you can see, this is determined by the height of each layer of conductor, h1and h2, multiplied by 1/3, and by the thickness of the insulating material, hins. For a bobbin-wound construction, the length of the winding lis given by the distance from one end of the bobbin to the other. The equation tells us that a wide bobbin will reduce leakage inductance, so it can be important to look for a longer dimension here when selecting your core and bobbin type.
Thin wire buildup will also reduce leakage, as will a minimum amount of insulation material between primary and secondary windings. However, the insulation must meet full safety requirements, so it is not possible to make this dimension zero. We need to worry about voltage breakdown from one winding to another. Even with this requirement, typical dimensions for the insulation thickness are very small – much less than 1 mm, and this is crucial to low-leakage designs.
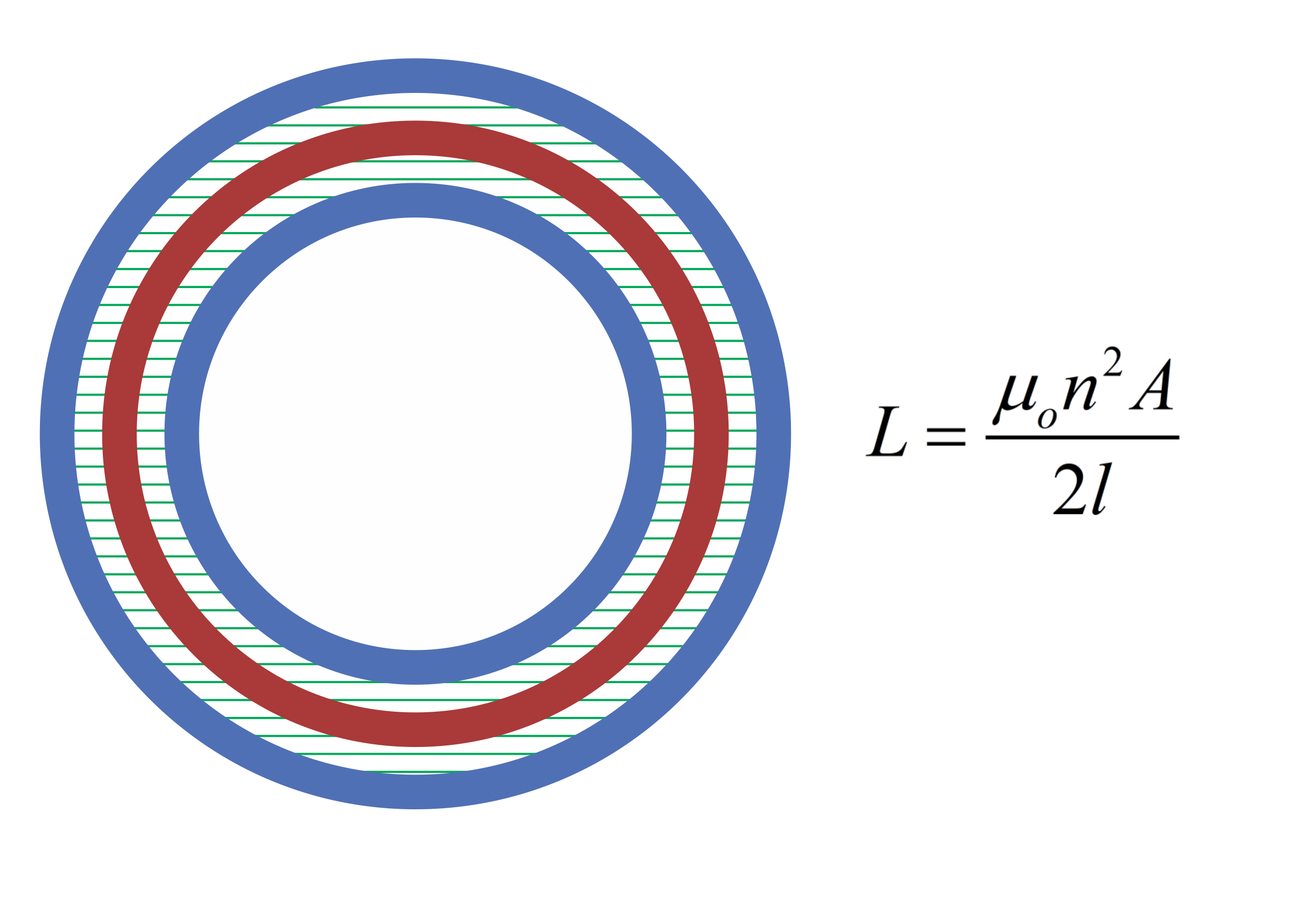
Another technique for reducing the leakage of a transformer is by adding additional windings, as shown in Figure 6. This is also referred to as interleaving – winding a secondary, then a primary, then another secondary will cut the leakage inductance down by a factor of two. There are endless variations to accomplish this. Some designers are fond of PC Board transformers, or planar transformers, where multiple primaries are alternated with multiple secondaries in order to cut the leakage inductance. More experienced and pragmatic designers recognize that you can go too far. Too small a leakage can present different problems to circuit operation, especially when you combine this with the increase in capacitance that goes along with each additional layer of winding. There is no set solution for every design.
Figure 6: Adding an Additional Primary or Secondary Winding Reduces Leakage Inductance by a Factor of Two
Designing for Leakage Inductance
If you have a design with too much leakage inductance, the equation tells you that the most powerful way to reduce it is by reducing the turns count. If you can cut the turns in half, the leakage goes down by a factor of 4. This is the single most important factor in designing low leakage transformers – keep the turns count low. At the same time, of course, you must obey the one equation to not saturate the core.
Of course, the equation given for leakage inductance in this article is an approximation. Realistically, we don’t have quite the same situation as a long solenoid. There will be end effects, uneven spacing of wires and terminations. Measurement of the leakage inductance is a crucial design step, and even the lowest-cost manufacturers willattempt to measure this component. The accuracy of that measurement will be discussed in future articles, and you can also read about that in Reference [2].
When making measurements or assessing a vendor’s measurements, beware of one of the common traps of transformer design, shown in Figure 7. There is a widely held belief that the leakage of a transformer should be about 1% of the magnetizing inductance, but this is a total myth. Sometimes you may coincidentally be at about this number if you have a gapped transformer (ina flyback transformer, for example). However, if your transformer is ungapped, it is not uncommon to measure a leakage inductance which can be 0.1% of the magnetizing inductance. Modern core materials have high relative permeability, in the order of several thousand. The core permeability only affects the magnetizing inductance, not the leakage, so you can see how the ratio of 1% is a very arbitrary number.
Leakage inductance is more than just a number to predict how well the transformer will work in the circuit. If you give a small tolerance, perhaps 20%, for the leakage measurement, this will ensure that the transformer is being repeatably built.
Figure 7: One of the Very Misleading Assumptions About Leakage Inductance. Don’t fall into this trap.
Now, finally, we can move on to the design implications of power transformers for hard-switched converters. As we saw for the full-bridge design at the beginning of the article, there was NO freedom of choice for turns count on the transformer. For this, and every higher power design at relatively low output voltage, the secondary is just a single turn. There is no consideration of window-area product, current-density, fill factor, or any of the other common quantities that text books may suggest for design to an “optimum” point. We just set the secondary turn to one, and this defines the rest of the design.
The single secondary turn then is multiplied by the needed turns ratio for the converter to operate properly at low line in order to get the primary turns count. This is used with the single transformer design equation that we found in the previous article, repeated in Figure 8.
Figure 8: The Single Transformer Design Equation. With the secondary turns count set to one, there is no design freedom for the transformer core area.
Single Turns at Higher Frequencies
We can see that for an 850 W design, we run into the single turn limit for a transformer at just 100 kHz. This is for a 5-V output. If the output were 12 V, we would have the option of a single turn, or perhaps just two turns. Both of these should be tested in a paper design, and probably also in hardware.
With the availability of new devices, we are seeing switching frequencies rising in the industry. It is not uncommon to see a 500 W design switching at 200-500 kHz, or even higher. But the secondary count is still frozen at a single turn, which means that there can be limited benefits to continued increase in frequency. This is one of the reasons that the frequency has not jumped as high as originally promised by the new wide-bandgap technologies.
In many designs, the increase in frequency is accompanied by a change to soft-switching technology such as the LLC or phase-shifted bridge. The leakage of the transformer then becomes part of the circuit operation and the need for very low leakage design is changed.
Some extreme density designs take the switching frequency into the MHz range. This does not make sense if the transformer secondary turns count is still stuck at 1 turn. This takes us into the realm of matrix transformers where fractional turns designs can be achieved. This is beyond the scope of this article, but it is a technology that will be part of the roadmap forward for power conversion.
Summary
One equation governs the saturation of a transformer, but the leakage inductance provides strong direction to a design. It must be taken into consideration early in the design procedure to avoid problems in the power circuit. For hard-switched converters, high leakage produces excessive ringing. For soft-switched converters, the leakage becomes part of the resonant tank and must be carefully controlled.
For low output voltage, the secondary turns frequently run into the limit of a single turn, and the entire transformer design process starts at that point in order to minimize the leakage.
References
-
Magnetics Design Videos and Articles, Ridley Engineering Design Center.
-
Measuring transformer impedance, http://ridleyengineering.com/design-center-ridley-engineering/39-magnetics/80-046-transformer-impedance-measurements.html
-
RidleyWorks™ design software contains complete magnetics design and advanced analysis. A free Buck Designer is available for download.
-
Learn about proximity losses and magnetics design in our hands-on workshops for power supply design www.ridleyengineering.com/workshops.html This is the only hands-on magnetics seminar in the world.
-
Join over 300 engineers on our Facebook group titled Power Supply Design Center. Advanced in-depth discussion groupfor all topics related to power supply design.